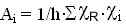Ge 214: Pyroxene homework series: part II

Energy states of Fe²⁺ in C_2v symmetry in the M2 site

We know from Tanabe-Sugano energy level diagrams in Cotton, Burns, or any other reference, that Fe²⁺ has two energy states in an octahedral environment, namely T_2g and E_g . What the energy level diagrams do not tell us is what are the states of the Fe²⁺ system when it is in a lower symmetry such as C_2v. We are going to have to work this out. Because both the T and E states are degenerate, we should suspect that these degeneracies might be lifted in the lower symmetry. This will be a moderately long, but not particularly complicated process.

1) We would already know the answer to the problem if the Fe²⁺ M(2) site were still an octahedron. Our plan is to start with this knowledge and to see how the octahedral states split when the site is changed to the lower symmetry. First we must determine which symmetry elements originally present in octahedral symmetry are still preserved in C_2v symmetry. Because the C_2v site can be directly derived from the octahedral site by simple geometric distortion without adding or subtracting atoms, and without breaking bonds (topologically identical sites), it should be evident that the symmetry elements of the C_2v site are a subset of the symmetry elements of the octahedral site. But how to determine which ones are preserved?

We can work this out in full detail via the methods explained in chapter 9 of Cotton. I will ask you to proceed along a less detailed route which makes use of the symmetry properties of the site and the information about symmetry encoded in the character tables.

Our primary problem is that a coordinate transformation has occurred in going from the O_h to the C_2v site. Note that the oxygen atoms are on the x, y and z axes of the O_h site, but the z (C₂) axis of C_2vbisects the Fe-O bond axes. To determine which symmetry elements in O_h symmetry are preserved in C_2v symmetry, pretend that the O-Fe-O bond angles are 89.99° in the M(2) site. Establish (draw) the coordinate system for an octahedral site, mentally place the M(2) site on top of it, and rotate the M(2) symmetry coordinate system so that the site is oriented along the octahedral symmetry axes; that is to say, rotate the site until the Fe-O bonds are placed along the octahedral axes. There are a number of ways you can do this (the x, y, and z axes in O_h are equivalent); they will all lead to the same answer. Just so we all do it the same way, put the C₂ axis of the C_2v site in the horizontal plane of the octahedral coordinate system.

Now identify and list the symmetry elements that are preserved. The symmetry elements of O_hare listed on the top of the character table for O_h.

2) The next step is to use our knowledge of the remaining symmetry elements and the states which exist in octahedral symmetry to derive the states of Fe²⁺ in the low symmetry M(2) site. Construct a subset of the octahedral character table with just the following entries: T₂ and E_g (the only two states of interest from octahedral Fe²⁺) and just the symmetry elements which are preserved in C_2v symmetry. These are the only symmetry elements and entries in the character table with which we must be concerned. If we can solve the problem for this subset, we will have solved it for C_2v.

From the character tables, we need to look at the character of T_2g and E_g states in O_h and see into what they factor in C_2v.
In other words, what linear combination of the rows in the C_2vcharacter table to we need to add together to get the characters for the T_2gentry?

You should have the following character table for the elememts of O_hthat remain in C_2v. This is the reducible representation.

Now look at the C_2v character table and determine what two rows for that table must be added together to give the row for E_g in the table just above. You can easily do this by trial and error. Next do it for the T_2gentry. You should be able to do this by trial and error, or you can use the formula 4.3-11 in Cotton's book (1971 addition).

which gives the number times the a_i^thirreducible representation occurs in a reducible representation.

h = the order of the group = the number of elements in the group.
e.g. in C_2v, h = 1 E + 1 C₂ + 1 sigma(h) + 1 sigma(d) = 4

XR = the character of the reducible representation
e.g. for E, XR = 3
Xi = the character of the i^th irreducible representation.
e.g. in C_2v, for E, Xi = 1

So, the number of A₁ states in C_2v that derive from T_2g is
A₁ = 1/4×[3×1 + 1×1 + (-1)×1 + 1×1] = 4/4 = 1

After doing this for all the possible states, you will determine the states into which T_2g and E_g split in C_2v.
But, you will still not know the energies of the states. We need to go experimental data at this point.

We will use a low-iron enstatite where iron in the M(2) site dominates the spectrum.

The Experimentally Determined Energy states of Fe²⁺ in C_2v symmetry.

We will again examine the experimental spectroscopic data for Fe²⁺ in orthopyroxene to get a feel for what it is we still need to do. The prominent features of the data are band splitting and polarizations. The previous parts of the homework derived the fact that the splittings should occur. Next we have to deal with the polarizations.

1) Read section 5.41 in Burns, Mineralogical Applications of Crystal Field Theory (1970), which will give you some of the experimental data. The analysis that follows has been rendered out of date by later work on the west coast.

2) Attached, are two orthopyroxene spectra.

The first figure 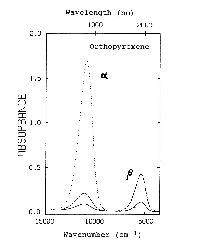shows the alpha (dots), beta (dash) and gamma (solid line) spectra of a 100 micrometer thick bronzite (Fs₁₄) in the visible and near-infrared range.

The second figure 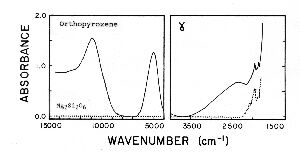shows only the gamma spectrum of two 0.5 mm thick crystals in the visible through the mid-infrared range. The solid line is for hypersthene (Fs_39.5), and the dotted line is for synthetic enstatite (Fs_0.00).

Compile a list of band positions and polarizations of all Fe²⁺bands (both in terms of the indicatrix direction and in terms of the morphological axes). Also determine the molar absorptivity (epsilon parameter) for each band.

The Origin of Polarizations and Pleochroism.

We will use the observed polarization properties of the Fe²⁺spectrum in the pyroxene M(2) site to establish the order of the C_2v states. To do this, we must first establish some predictions about the polarization dependence of each possible electronic transition. We will then compare our predictions (models) to the actual data and hope that afterwards, only a single model will remain viable.

1) Electronic transitions, in general are polarized. They correspond to a redistribution of electronic charge in three-dimensional space. These redistributions of electrons have vector properties and must match the electric dipole of the exciting radiation if there is to be effective coupling of energy between the incident radiation and the electron cloud.

Here is picture of two orthopyroxene crystals that show the visible-wavelength anisotropy when viewed in linerally polarized light. As you can see from the spectra above, the anisotropy is much more pronounced in the near-infared region.

We want to know the polarizations of transitions such as:

Ground State -> Excited State

That is to say, we want to know along which C_2v molecular axis (or axes) a particular electronic transition (such as A₁-> B₁) will occur. Once we know this, we need only to align a linear polarizer in this direction to make the transition occur (this assumes that we know the orientation of the molecular axes with respect to the morphological axes of the crystal).

Quantum mechanics tells us the intensity of an electronic transition will be proportional to an integral of the form:

m is an operator that corresponds to the components of an electric dipole having the form:

m = (k₁ • X + k₂ • Y + k₃ • Z)

where X, Y, and Z are the molecular axes.

We want to evaluate integrals of the form:

or by components:

From purely symmetry considerations, we can tell if the integrals are nonzero. This is analogous to evaluation of integrals of the odd (sine) and even (cos) functions.

Assume for a moment that the A₁state is the ground state. (Actually, ground states are often A₁states) We need to evaluate a whole series of integrals of the type:

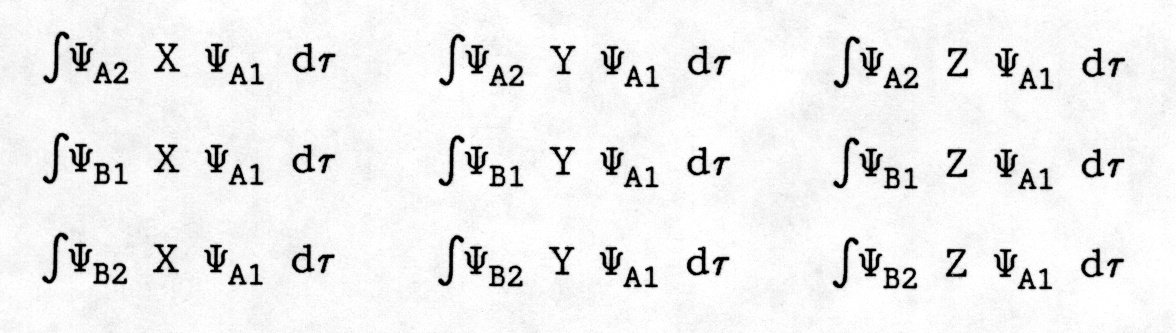
Where A1, B1, A2, and B2 are the designations for all the possible states.

Because A1, B1, A2, and B2 are not only designations for the possible states but are also the designation for their symmetry, we can forget the details of the (complicated) mathematical descriptions of the wavefunctions, and can instead cnocentrate ONLY on the symmetry properties.

Thus we need to evaluate integrals of the type:

From the character table, we learn that the molecular z axis in C_2v has the symmetry Al. (You can work this out by going through all the symmetry operations with the axis [+ and - lobes, don’t forget] or you can read it directly from the character table; the letter z in the Al row indicates that anything which is mathematically described by a function first order in just z [such as the z axis which is, after all, just +z] has Al symmetry.)

Thus, we need to evaluate integral (1) which has components with the symmetry property:

A2 •Al • Al

Is this integral non-zero?

Here is how we proceed:

We need to work out a multiplication table for C_2v wherein we multiply all possible symmetries by each other. Take the case of

A2 • Al • Al

We can do this with pairs of functions: (A2 • Al) • Al

This answer is equivalent to A2. In fact, you can show that Al times anything else is the something else.

Our problem of evaluating (A2 • Al) • Al has now been reduced to one of evaluating (A2) • Al

We already know the answer to this is A2.

In order for the integral to be non-zero, the integrand must be invarient under the operation of the symmetry elements for the group. This demands that the totally symmetric representation (Al) must be a component of the integrand. (This comes back to the even, odd function problem; we now are just worried about it in three dimensions).

Thus, we can now conclude that the transition from an Al state to an A2 state will not occur if it is stimulated with linearly polarized light vibration in the direction of the molecular Z axis.

You work out the answer for the X and Y components of this transition. You should now conclude that this transition is not allowed for any vibration direction of linearly polarized light. It is forbidden.

Now work out the answer for all three components of a possible transition from a) an Al state to an A2 state.

b) an Al state to a Bl state.

c) an Al state to a B2 state.

As you can now see, only one polarization component is allowed for each of these possible transitions.

2) Work out the multiplication table for all possible pairs of symmetry elements. Fill in the rest of the table

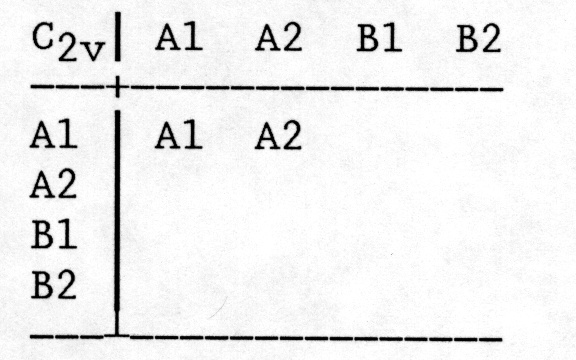
This will allow you to fill in the remaining entries in the following table which states the polarization directions for all possible transitions in C_2v.

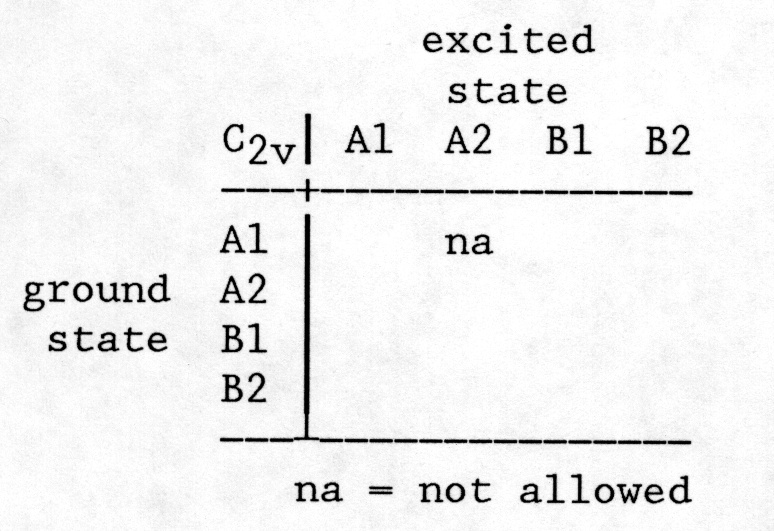
Our final step will be interpret the experimental data on the basis of our theoretical modeling.

Comparison of Models to Real Data

1) Notice that the highest energy absorption band is polarized in the a direction of the indicatrix. Use your projections of the crystal structure to establish which molecular axis of the C_2v M(2) site is oriented exactly on (or at least close to) the a direction.

2) Now use your table of selection rules (polarizations) from above to list all possible transitions which are polarized along the molecular axis closest to the a indicatrix direction. These are the candidates for the transition: ground state to the highest excited state. Can you establish which transition is the actual one in these orthopyroxenes? (Hint, the answer is yes.) Do it.

3) Once you have identified the states involved in the highest energy transition, you have established the ground state of Fe²⁺ in this site. From the polarization data you should be able to assign the remaining experimentally observed transitions to particular excited states. Construct an energy level diagram for Fe²⁺ in the M(2) site where the energy scale in linear and to scale, where the states are identified, and the polarization rules indicated for each state.

4) We have one state left over and unaccounted for. This remaining state has not yet been experimentally detected. It would be buried under intense infrared vibrational modes that dominate the infrared spectrum. You can read about where some theoretical calculations predicted it should be in the article by Goldmann and Rossman (1977) The spectra of iron in orthopyroxene revisited: the splitting of the ground state. American Mineralogist, 62, 151-157.

Another source for some more information on the spectroscopy of pyroxenes is in the Reviews of Mineralogy series, Volume 7, CT Prewitt, editor, Pyroxenes, chapter 3, Pyroxene Spectroscopy