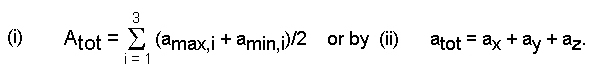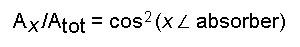Division
of Geological and
Planetary
Sciences, California Institute of Technology
Pasadena, CA 91125-2500 U.S.A.
The
absorbance in isotropic
material is linearly dependent on
the concentration of the absorber and on the thickness of the
sample
(A = e
· c · t). Measurement of absorbance
in anisotropic media is more complicated, but it can be obtained
from polarized spectra (i) on three random, but orthogonal
sections of a crystal, or (ii) preferably on two orthogonal
sections oriented parallel to each of two axes of the indicatrix
ellipsoid. To compare among different crystal classes (including
cubic symmetry) it is useful to convert measured absorbance
values to one common basis (the total absorbance
Atot),
wherein all absorbers are corrected as if they were aligned
parallel to the
E-vector
of the incident light. The total
absorption coefficient
(atot
= Atot/t)
is
calculated by
Only in special
circumstances will unpolarized measurements
of absorbance provide data useful for quantitative studies of
anisotropic material.
The orientation
of the absorber with respect to the axes of
the indicatrix ellipsoid is calculated according to
and analogously for
Ay and
Az.
In this way, correct angles are obtained for all cases of
symmetry.